Quasi harmonic approximation

Quasi harmonic approximation#

Usage of phonopy-qha#

Using phonopy results of thermal properties, thermal expansion and heat capacity at constant pressure can be calculated under the quasi-harmonic approximation. phonopy-qha is the script to run fitting and calculation to perform it. Mind that at leave 5 volume points are needed to run phonopy-qha for fitting.

An example of the usage for example/Si-QHA is as follows.

To watch selected plots:

% phonopy-qha -p e-v.dat thermal_properties.yaml-{-{5..1},{0..5}}
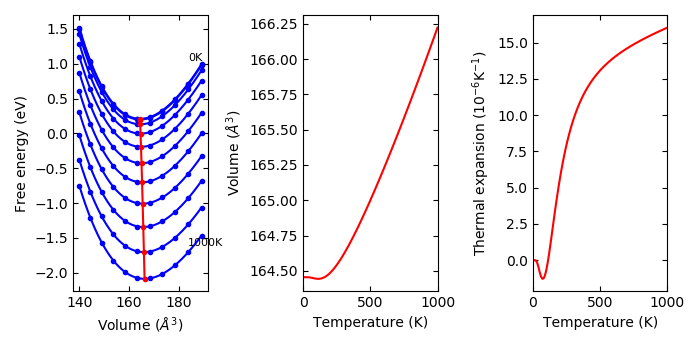
_images/Si-QHA.png

Without plots:

% phonopy-qha e-v.dat thermal_properties.yaml-{-{5..1},{0..5}}

The first argument is the filename of volume-energy data (in the above example, e-v.dat). The volumes and energies are given in \(\text{Angstrom}^3\) and eV, respectively. Theses energies are only dependent on volume but not on temperature unless using --efe option. Therefore in the simplest case, these are taken as the electronic total energies at 0K. An example of the volume-energy file is:

#   cell volume   energy of cell other than phonon
     140.030000           -42.132246
     144.500000           -42.600974
     149.060000           -42.949142
     153.720000           -43.188162
     158.470000           -43.326751
     163.320000           -43.375124
     168.270000           -43.339884
     173.320000           -43.230619
     178.470000           -43.054343
     183.720000           -42.817825
     189.070000           -42.527932

Lines starting with # are ignored.

The following arguments of phonopy-qha are the filenames of thermal_properties.yaml’s calculated at the volumes given in the volume-energy file. These filenames have to be ordered in the same order as the volumes written in the volume-energy file. Since the volume v.s. free energy fitting is done at each temperature given in thermal_properties.yaml, all thermal_properties.yaml’s have to be calculated in the same temperature ranges and with the same temperature step. phonopy-qha can calculate thermal properties at constant pressure up to the temperature point that is one point less than that in thermal_properties.yaml because of the numerical differentiation with respect to temperature points. Therefore thermal_properties.yaml has to be calculated up to higher temperatures than that expected by phonopy-qha.

Another example for Aluminum is found in the example/Al-QHA directory.

If the condition under pressure is expected, \(PV\) terms may be included in the energies, or equivalent effect is applied using --pressure option.

Experimentally, temperature dependent energies are supported by --efe option. The usage is written at phonopy/phonopy.

Options#

-h#

Show help. The available options are shown. Without any option, the results are saved into text files in simple data format.

--tmax#

The maximum temperature calculated is specified. This temperature has to be lower than the maximum temperature calculated in thermal_properties.yaml to let at least one temperature points fewer. The default value is --tmax=1000.

--pressure#

Pressure is specified in GPa. This corresponds to the \(pV\) term described in the following section Thermal properties in (T, p) space calculated under QHA. Note that bulk modulus obtained with this option than 0 GPa is incorrect.

-b#

Fitting volume-energy data to an EOS, and show bulk modulus (without considering phonons). This is made by:

% phonopy-qha -b e-v.dat

--eos#

EOS is chosen among vinet, birch_murnaghan, and murnaghan. The default EOS is vinet.

% phonopy-qha --eos='birch_murnaghan' -b e-v.dat

-p#

The fitting results, volume-temperature relation, and thermal expansion coefficient are plotted on the display.

-s#

The calculated values are written into files.

--sparse#

This is used with -s or -p to thin out the number of plots of the fitting results at temperatures. For example with --sparse=10, 1 in 10 temperature curves is only plotted.

--efe#

Experimental

Temperature dependent energies other than phonon free energy are included with this option. This is used such as:

% phonopy-qha -p --tmax=1300 --efe fe-v.dat e-v.dat thermal_properties.yaml-{00..10}
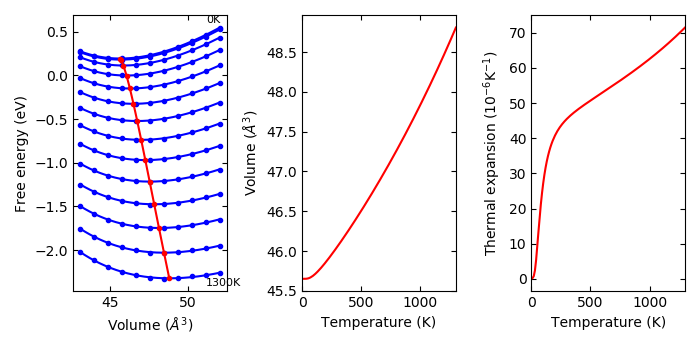
_images/Cu-QHA.png

The temperature dependent energies are stored in fe-v.dat. The file format is:

# volume:       43.08047896     43.97798894     44.87549882     45.77300889     46.67051887     47.56802885     48.46553883     49.36304881     50.26055878     51.15806876     52.05557874
#    T(K)     Free energies
    0.0000     -17.27885993    -17.32227490    -17.34336569    -17.34479760    -17.32843604    -17.29673896    -17.25081954    -17.19263337    -17.12356816    -17.04467997    -16.95752155
   10.0000     -17.27886659    -17.32228126    -17.34337279    -17.34481060    -17.32844885    -17.29675204    -17.25083261    -17.19264615    -17.12358094    -17.04469309    -16.95753464
   20.0000     -17.27887453    -17.32228804    -17.34338499    -17.34482383    -17.32846353    -17.29676491    -17.25084547    -17.19265900    -17.12359399    -17.04470709    -16.95754774
...

The first column gives temperatures in K and the following columns give electronic free energies in eV at temperatures and at unit (primitive) cell volumes. The lines starting with # are ignored. This file doesn’t contain the information about cell volumes. Instead, the volumes are obtained from e-v.dat file. The energies in e-v.dat are not used when --efe option is used. The temperature points are expected to be the same as those in thermal_properties.yaml at least up to the maximum temperature specified for phonopy-qha.

An example is given in example/Cu-QHA. The fe-v.dat contains electronic free energy calculated following, e.g., Eqs. (11) and (12) in the paper by Wolverton and Zunger, Phys. Rev. B, 52, 8813 (1994) (of course this paper is not the first one that showed these equations):

\[S_\text{el}(V) = -gk_{\mathrm{B}}\Sigma_i \{ f_i(V) \ln f_i(V) + [1-f_i(V)]\ln [1-f_i(V)] \}\]

with

\[f_i(V) = \left\{ 1 + \exp\left[\frac{\epsilon_i(V) - \mu(V)}{T}\right] \right\}^{-1}\]

and

\[E_\text{el}(V) = g\sum_i f_i(V) \epsilon_i(V),\]

where \(g\) is 1 or 2 for collinear spin polarized and non-spin polarized systems, respectively. For VASP, a script to create fe-v.dat and e-v.dat by these equations is prepared as phonopy-vasp-efe, which is used as:

% phonopy-vasp-efe --tmax=1500 vasprun.xml-{00..10}

where vasprun.xml-{00..10} have to be computed for the same unit cells as those used for thermal_properties.yaml. When phonopy was run with PRIMITIVE_AXES or --pa option, the unit cells for computing electronic eigenvalues have to be carefully chosen to agree with those after applying PRIMITIVE_AXES, or energies are scaled a posteriori.

Output files#

The physical units of V and T are \(\text{Angstrom}^3\) and K, respectively. The unit of eV for Helmholtz and Gibbs energies, J/K/mol for \(C_V\) and entropy, GPa for for bulk modulus and pressure are used.

  • Bulk modulus \(B_T\) (GPa) vs \(T\) (bulk_modulus-temperature.*)

  • Gibbs free energy \(G\) (eV) vs \(T\) (gibbs-temperature.*)

  • Heat capacity at constant pressure \(C_p\) (J/K/mol) vs \(T\) computed by \(-T\frac{\partial^2 G}{\partial T^2}\) from three \(G(T)\) points (Cp-temperature.*)

  • Heat capacity at constant pressure \(C_p\) (J/K/mol) vs \(T\) computed by polynomial fittings of \(C_V(V)\) (Cv-volume.dat) and \(S(V)\) (entropy-volume.dat) for \(\partial S/\partial V\) (dsdv-temperature.dat) and numerical differentiation of \(\partial V/\partial T\), e.g., see Eq.(5) of PRB 81, 174301 by Togo et al. (Cp-temperature_polyfit.*). This may give smoother \(C_p\) than that from \(-T\frac{\partial^2 G}{\partial T^2}\).

  • Volumetric thermal expansion coefficient \(\beta\) vs \(T\) computed by numerical differentiation (thermal_expansion.*)

  • Volume vs \(T\) (volume-temperature.*)

  • Thermodynamics Grüneisen parameter \(\gamma = V\beta B_T/C_V\) (no unit) vs \(T\) (gruneisen-temperature.dat)

  • Helmholtz free energy (eV) vs volume (helmholtz-volume.*). When --pressure option is specified, energy offset of \(pV\) is added. See also the following section (Thermal properties in (T, p) space calculated under QHA).

Thermal properties in (T, p) space calculated under QHA#

Here the word ‘quasi-harmonic approximation’ is used for an approximation that introduces volume dependence of phonon frequencies as a part of anharmonic effect.

A part of temperature effect can be included into total energy of electronic structure through phonon (Helmholtz) free energy at constant volume. But what we want to know is thermal properties at constant pressure. We need some transformation from function of V to function of p. Gibbs free energy is defined at a constant pressure by the transformation:

\[G(T, p) = \min_V \left[ U(V) + F_\mathrm{phonon}(T;\,V) + pV \right],\]

where

\[\min_V[ \text{function of } V ]\]

means to find unique minimum value in the brackets by changing volume. Since volume dependencies of energies in electronic and phonon structures are different, volume giving the minimum value of the energy function in the square brackets shifts from the value calculated only from electronic structure even at 0 K. By increasing temperature, the volume dependence of phonon free energy changes, then the equilibrium volume at temperatures changes. This is considered as thermal expansion under this approximation.

phonopy-qha collects the values at volumes and transforms into the thermal properties at constant pressure.