Direct solution of linearized phonon Boltzmann equation#
This page explains how to use the direct solution of LBTE by L. Chaput, Phys. Rev. Lett. 110, 265506 (2013) (citation).
How to use#
As written in the following sections, this calculation requires large memory
space. When running multiple temperature points, simply the memory space needed
is multiplied by the number of the temperature points. Therefore it is normally
recommended to specify –ts option. An example to run with
the direct solution of LBTE for example/Si-PBEsol is as follows:
% phono3py-load --mesh 11 11 11 --lbte --ts 300
...
=================== End of collection of collisions ===================
- Averaging collision matrix elements by phonon degeneracy [0.036s]
- Making collision matrix symmetric (built-in) [0.001s]
----------- Thermal conductivity (W/m-k) with tetrahedron method -----------
Diagonalizing by lapacke dsyev... [0.141s]
Calculating pseudo-inv with cutoff=1.0e-08 (np.dot) [0.001s]
# T(K) xx yy zz yz xz xy
300.0 113.140 113.140 113.140 0.000 0.000 -0.000
(RTA) 108.982 108.982 108.982 0.000 0.000 -0.000
----------------------------------------------------------------------------
Thermal conductivity and related properties were written into
"kappa-m111111.hdf5".
Eigenvalues of collision matrix were written into "coleigs-m111111.hdf5"
...
Memory usage#
The direct solution of LBTE needs diagonalization of a large collision matrix, which requires large memory space. This is the largest limitation of using this method. The memory size needed for one collision matrix at a temperature point is \((\text{number of irreducible grid points} \times \text{number of bands} \times 3)^2\) for the symmetrized collision matrix.
These collision matrices contain real values and are supposed to be 64bit float
symmetric matrices. During the diagonalization of each collision matrix with
LAPACK dsyev solver, around 1.2 times more memory space is consumed in total.
When phono3py runs with –wgp option together with --lbte
option, estimated memory space needed for storing collision matrix is presented.
An example for example/Si-PBEsol is as follows:
% phono3py-load --mesh 40 40 40 --lbte --wgp
...
Memory requirements:
- Piece of collision matrix at each grid point, temp and sigma: 0.00 Gb
- Full collision matrix at each temp and sigma: 7.15 Gb
- Phonons: 0.04 Gb
- Grid point information: 0.00 Gb
- Phonon properties: 0.14 Gb
...
With –stp option, estimated memory space needed for ph-ph interaction strengths is shown such as
% phono3py-load --mesh 40 40 40 --lbte --stp
Work load distribution#
The other difficulty compared with RTA is the workload distribution. Currently there are two ways to distribute the calculation: (1) Collision matrix is divided and the pieces are distributed into computing nodes. (2) Ph-ph interaction strengths at grid points are distributed into computing nodes. These two can not be mixed, so one of them has to be chosen. In either case, the distribution is done simply running a set of phono3py calculations over grid points and optionally band indices. The data computed on each computing node are stored in an hdf5 file. Increasing the calculation size, e.g., larger mesh numbers or larger number of atoms in the primitive cell, large files are created.
Distribution of collision matrix#
A full collision matrix is divided into pieces at grid points of irreducible part of Brillouin zone. Each piece is calculated independently from the other pieces. After finishing the calculations of these pieces, the full collision matrix is diagonzalized to obtain the thermal conductivity.
File size of Each piece of the collision matrix can be large. Therefore it is
recommended to use –ts option to limit the number of
temperature points, e.g., --ts "100 200 300 400 500", depending on the memory
size installed on each computing node. To write them into files,
--write-collision option must be specified, and to read them from files,
--read-collision option is used. These are similarly used as
–write-gamma and
–read-gamma options for RTA calculation as shown in
Workload distribution. --read-collision option collects the pieces and
make one full collision matrix, then starts to diagonalize it. This option
requires one argument to specify an index to read the collision matrix at one
temperature point, e.g., the collision matrix at 200K is read with
--read-collision 1 for the (pieces of) collision matrices created with
--ts "100 200 300 400 500" (corresponding to 0, 1, 2, 3, 4). The temperature
(e.g. 200K) is also read from the file, so it is unnecessary to specify
–ts option when reading.
The summary of the procedure is as follows:
Running at each grid point with –gp (or –ga) option and saving the piece of the collision matrix to an hdf5 file with
--write-collisionoption. It is probably OK to calculate and store the pieces of the collision matrices at multiple temperatures though it depends on memory size of the computer node. This calculation has to be done at all irreducible grid points.Collecting and creating all necessary pieces of the collision matrix with
--read-collision=num(num: index of temperature). By this one full collision matrix at the selected temperature is created and then diagonalized. An option-o nummay be used together with--read-collisionto distinguish the file names of the results at different temperatures.
Examples of command options are shown below using Si-PBE example. Irreducible
grid point indices are obtained by –wgp option:
% phono3py-load --mesh 19 19 19 --lbte --wgp
and the information is given in ir_grid_points.yaml. For distribution of
collision matrix calculation (see also Workload distribution):
% phono3py-load --mesh 19 19 19 --lbte --ts 300 --write-collision --gp="grid_point_numbers..."
To collect distributed pieces of the collision matrix:
% phono3py-load --mesh 19 19 19 --lbte --read-collision 0
where --read-collision 0 indicates to read the first result in the list of
temperatures by --ts option, i.e., 300K in this case.
Distribution of phonon-phonon interaction strengths#
The distribution of pieces of collision matrix is straightforward and is
recommended to use if the number of temperature points is small. However
increasing data file size, network communication becomes to require long time to
send the files from a master node to computation nodes. In this case, the
distribution over ph-ph interaction strengths can be another choice. Since,
without using –full-pp option, the tetrahedron method
or smearing approach with –sigma-cutoff option
results in the sparse ph-ph interaction strength data array, i.e., most of the
elements are zero, the data size can be reduced by only storing non-zero
elements. Not like the collision matrix, the ph-ph interaction strengths in
phono3py are independent from temperature though it is not the case if the force
constants provided are temperature dependent. Once stored, they are used to
create the collision matrices at temperatures. Using --write-pp and
--read-pp, they are written into and read from hdf5 files at grid points.
It is also recommended to use –write-phonon option and –read-phonon option to use identical phonon eigenvectors among the distributed nodes.
The summary of the procedure is as follows:
Running at each grid point with –gp (or –ga) option and storing the ph-ph interaction strengths to an hdf5 file with
--write-ppoption. This calculation has to be done at all irreducible grid points.Running with
--read-ppoption and without –gp (or –ga) option. By this one full collision matrix at the selected temperature is created and then diagonalized. An option-o nummay be used together with--read-collisionto distinguish the file names of the results at different temperatures.
Examples of command options are shown below using Si-PBE example. Irreducible
grid point indices are obtained by –wgp option
% phono3py-load --mesh "19 19 19" --lbte --wgp
and the grid point information is provided in ir_grid_points.yaml. All phonons
on mesh grid points are saved by
% phono3py-load --mesh "19 19 19" --write-phonon
For distribution of ph-ph interaction strength calculation (see also Workload distribution)
% phono3py-load --mesh "19 19 19" --lbte --ts 300 --write-pp --gp "grid_point_numbers..." --read-phonon
Here one temperature has to be specified but any one of temperatures is OK since ph-ph interaction strength computed here is assumed to be temperature independent. Then the computed ph-ph interaction strengths are read and used to compute collision matrix and lattice thermal conductivity at a temperature by
% phono3py-load --mesh "19 19 19" --lbte --ts 300 --read-pp --read-phonon
This last command is repeated at different temperatures to obtain the properties at multiple temperatures.
Cutoff parameter of pseudo inversion#
To achieve a pseudo inversion, a cutoff parameter is used to find null space,
i.e., to select the nearly zero eigenvalues. The default cutoff value is 1e-8,
and this hopefully works in many cases. But if a collision matrix is numerically
not very accurate, we may have to carefully choose the value by --pinv-cutoff
option. It is safer to plot the absolute values of eigenvalues in log scale to
see if there is clear gap between non-zero eigenvalue and nearly-zero
eigenvalues. After running the direct solution of LBTE, coleigs-mxxx.hdf5 is
created. This contains the eigenvalues of the collision matrix (either
symmetrized or non-symmetrized). The eigenvalues are plotted using
phono3py-coleigplot in the phono3py package:
% phono3py-coleigplot coleigs-mxxx.hdf5
It is assumed that only one set of eigenvalues at a temperature point is contained.
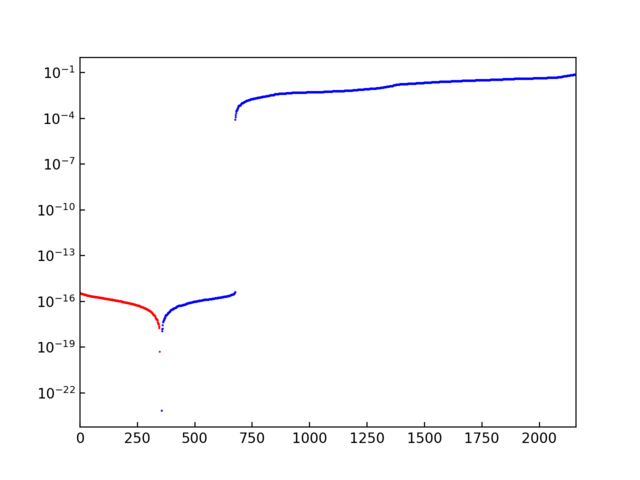
Eigenvalues are plotted in log scale (Si-PBEsol example with 15x15x15 mesh). The number in x-axis is just the index where each eigenvalue is stored. Normally the eigenvalues are stored ascending order. The blue points show the positive values, and the red points show the negative values as positive values (absolute values) to be able to plot in log scale. In this plot, we can see the gap between \(10^{-4}\) and \(10^{-16}\), which is a good sign. The values whose absolute values are smaller than \(10^{-8}\) are treated as 0 and those solutions are considered as null spaces.#
Diagonalization solver interfaces#
Multithreaded BLAS is recommended to use for the calculation of the direct solution of LBTE because the diagonalization of the collision matrix is computationally highly demanding. The diagonalization in Phono3py relies on LAPACK via BLAS library. There are choices of the BLAS libraries. OpenBLAS and MKL are considered most popular choices. For non-INTEL (or AMD) systems such as ARM64, MKL can not be used. How to choose the BLAS library in installation via conda-forge is written here.
Phono3py has two different interfaces to the LAPACK library. One is via scipy (or numpy), and the other is via LAPACKE as shown below. How to switch between interfaces is described in the next section.
OpenBLAS or MKL linked scipy and numpy#
Scipy and numpy have interfaces to LAPACK dsyevd, and scipy also has the
interface to dsyev. OpenBLAS and MKL linked scipy and numpy are provided by
conda-forge.
OpenBLAS or MKL via LAPACKE#
LAPACK dsyev and dsyevd can be accessed via LAPACKE in the phono3py’s C
language implementation through the python C-API.
Solver choice for diagonalization#
Diagonalizing the collision matrix for larger systems is the most time-consuming step and requires significant memory. Phono3py uses LAPACK for diagonalization, making performance highly dependent on the solver choice. Utilizing multithreaded BLAS on many-core nodes can significantly reduce computation time, allowing calculations to complete within practical limits. Currently, Phono3py supports diagonalization via scipy, numpy, and LAPACKE as LAPACK wrappers.
The default choice of the diagonalization solver is scipy.linalg.lapack.dsyev
(--pinv-solver=4). Using --pinv-solver NUMBER, one of the following solvers
is specified:
(Only available when compiling with LAPACKE) Lapacke
dsyev: Smaller memory consumption thandsyevd, but slower. This is the default solver when MKL LAPACKE is integrated or scipy is not installed.(Only available when compiling with LAPACKE) Lapacke
dsyevd: Larger memory consumption thandsyev, but faster. This is not considered as stable asdsyevbut can be significantly faster thandsyevfor solving large collision matrix. It is recommended to compare the result with that bydsyevsolver using smaller collision matrix (e.g., sparser sampling mesh) before starting solving large collision matrix.Numpy’s
dsyevd(linalg.eigh). Similar to solver (2), this solver should be used carefully.Scipy’s
dsyev: This is the default solver when scipy is installed and MKL LAPACKE is not integrated.Scipy’s
dsyevd: Similar to solver (2), this solver should be used carefully.